|
Problem 345. Equal circles, Tangents, Concurrent lines, Hexagon,
Semiperimeter. Level: High School, College, SAT Prep.
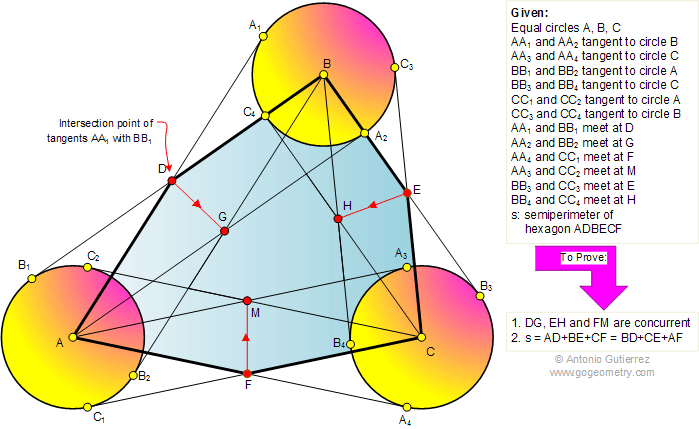
The figure shows equal circles A, B,
and C. AA1, AA2, CC3, and CC4
are tangents to circle B, AA3, AA4, BB3,
and BB4 are tangents to circle C, and BB1,
BB2, CC1, and CC2 are tangents
to circle A. Points D, E, F, G, H, and M are the intersection
points of the tangents AA1 with BB1, BB3
with CC3, AA4 with CC1, AA2
with BB2, BB4 with CC4, and AA3
with CC2, respectively. Prove that (1) The extension
of DG, EH, and FM are concurrent, (2) If s is the semiperimeter
of the hexagon ADBECF, then s = AD + BE + CF = BD + CE + AF.
|
Recent Additions
|