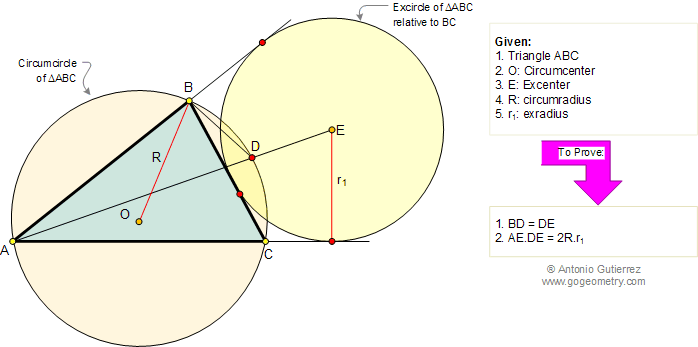
In the figure below, ABC is a triangle inscribed in a circle of center O (circumcenter) and E is the center (excenter) of the excircle relative to side BC. Line AE and the circumcircle meet at D. If R is the circumradius and r₁ is the exradius (radius of circle E), (1) prove that BD = DE, and (2) prove that AE.DE = 2R.r₁. View or post a solution.