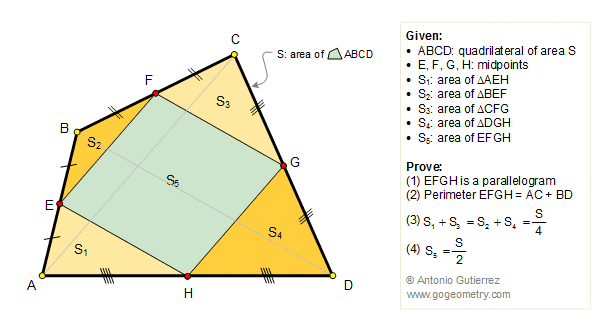
In the figure below, ABCD is a quadrilateral of area S. E, F, G, and H are the midpoints of the sides. If S1, S2, S3, and S4 are the areas of triangles AEH, BEF, CFG, and DGH respectively, (1) prove that EFGH is a parallelogram, called Varignon parallelogram, (2) prove that the perimeter of the Varignon parallelogram is equal to the sum of diagonals of ABCD, (3) prove that: , (4) prove that the area of the Varignon parallelogram is half that of ABCD.