Geometry Problem 143. Four Triangles, Incircle, Tangent and Parallel to Side, Circumradii

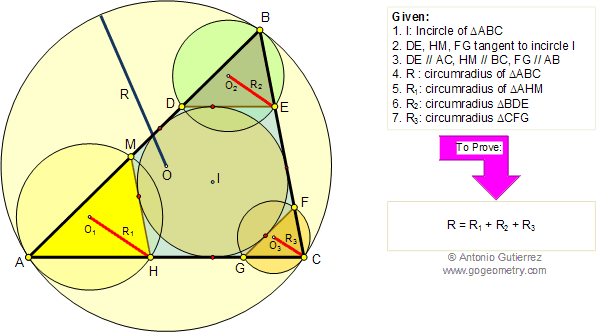
In the figure below, given a triangle ABC and the incircle of center I (inscribed circle), DE, FG, and HM are tangent to the incircle I and  parallel to AC, AB, and BC respectively. If R, R₁, R₂, R₃ are the circumradii of triangles ABC, AHM, BDE, and CFG respectively, prove that R = R₁ + R₂ + R₃. View or post a solution.