Geometry Problem 137. Orthic Triangle, Altitudes, Perpendicular, Incircle, Collinear Points, Parallelogram
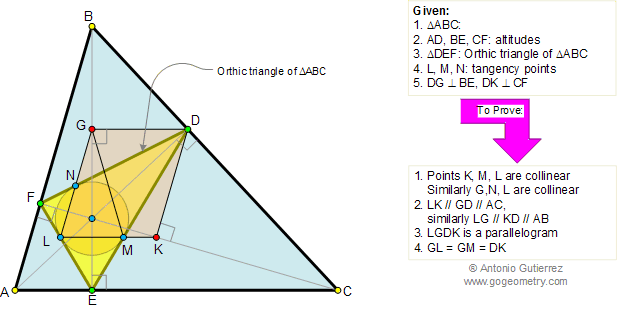
In the figure below, given a triangle
ABC and its orthic triangle DEF (AD, BE, and CF are the
altitudes of ABC). L, M, N
are the tangency points of the incircle of triangle DEF and DG and DK
are perpendicular to BE and CF respectively. (1) Prove that
points K, M, and L are collinear, similarly prove that points G,
N, and L are collinear, (2) prove that LK, GD, and AC are
parallel, similarly prove that LG, KD and AB are parallel, (3)
prove that LGDK is a parallelogram, and (4) prove that GL = GM =
DK.
View or post a solution
|