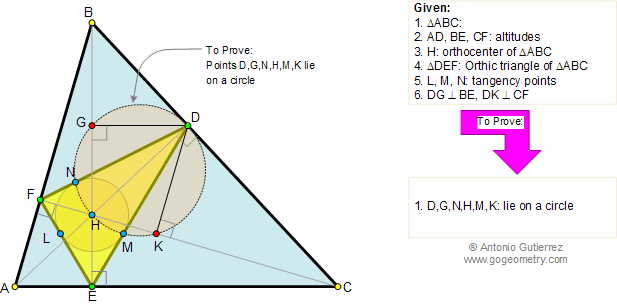
In the figure below, given a triangle ABC and its orthic triangle DEF (AD, BE, and CF are the altitudes of ABC). H is the orthocenter of triangle ABC, L, M, N are the tangency points of the incircle of triangle DEF and DG and DK are perpendicular to BE and CF respectively. Prove that D, G, N, H, M, and K are concyclic points (lie on a circle).