|
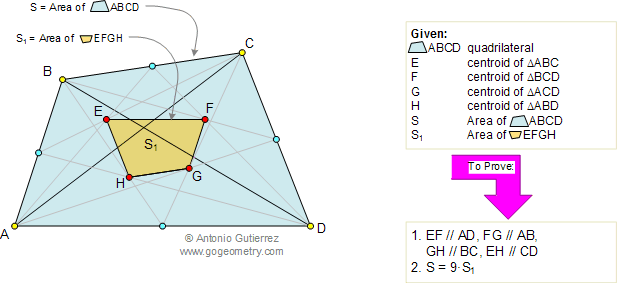
Consider the diagram below, which displays a quadrilateral ABCD of area S. The triangles ABC, BCD, ACD, and ABD have centroids E, F, G, and H respectively.
Let S1 be the area of the quadrilateral EFGH. It can be proven that (1) EF, FG, GH, and EH are parallel to AD, AB, BC, and CD respectively, and (2) S = 9S1.
View or post a solution.
.
Geometric shapes
Centroids, areas, similarity
A world of wonders
|
FACTS AND HINTS:
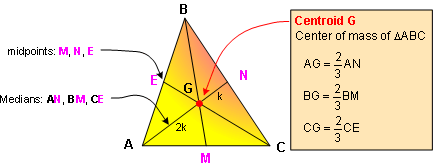
1. CENTROID:
The geometric centroid (center of mass) or barycenter of the
polygon vertices of a triangle is the point G which is also the
intersection of the triangle's three triangle medians.
Proposition: The centroid divides each of the medians in
the ratio 2:1
2. PROPORTIONAL SEGMENTS:
Proposition 1: If a line is parallel to one side of a
triangle, then it divides the other two sides proportionally.
Proposition 2: If a line divides two sides of a triangle
proportionally, it is parallel to the third side. (Converse of
-proposition 1.)
3. SIMILAR POLYGONS - Ratio of Areas:
Proposition: If two polygons are similar, the ratio of
their areas is equal to the square of the ratio of their
corresponding sides.
Home |
Geometry |
Search |
Problems |
Similarity |
Wolfram Demonstrations Project
|
Parallelograms
|
All Problems |
91-100 |
Visual
Index
|
Email |
View or post a solution | by Antonio Gutierrez
|