Geometry Tutoring Problem 97. Similar Triangles, Areas

Problem 97. Similar Triangles, Areas. Level: High School, SAT Prep, College

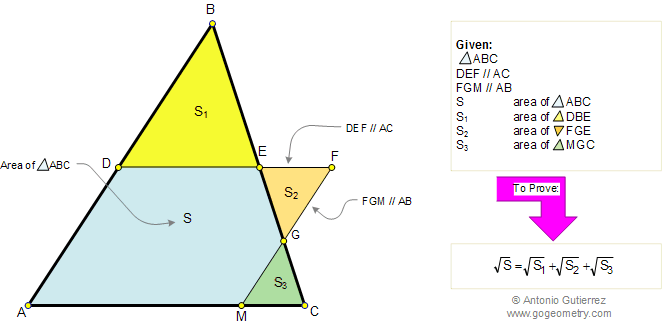
In the figure below, given a triangle ABC, line DEF parallel to AC and line FGM parallel to AB. If S, S₁, S₂, and S₃, are the areas of triangles ABC, DBE, FGE, and MGC respectively, prove that: \(\sqrt{S} = \sqrt{S_1} + \sqrt{S_2} + \sqrt{S_3}\). View or post a solution.

Problem about similar triangles and areas. Elearning

FACTS AND HINTS:

1. COMPARING AREAS OF SIMILAR TRIANGLES:
Proposition: The areas of similar triangles are to each other as the squares of any two corresponding segments.