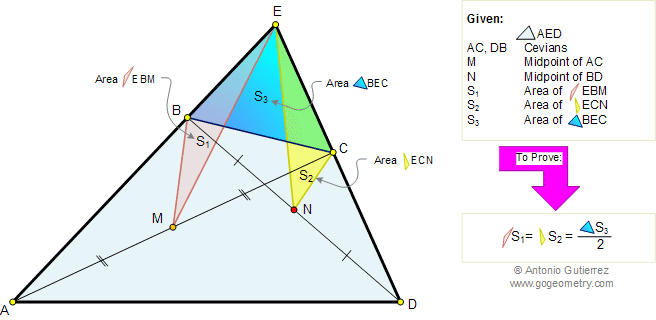
|
In the figure below, given a triangle
AED, M and N are the midpoints of cevians AC and DB
respectively. If S1, S2, and S3
are the areas of the triangles EBM, ECN, and BEC respectively,
prove that:
 .
"A great discovery solves a great problem, but there is a grain
of discovery in the solution of any problem. Your problem may be
modest, but if it challenges your curiosity and brings into play
your inventive faculties, and if you solve it by your own means,
you may experience the tension and enjoy the triumph of
discovery. Such expert experiences at a susceptible age may
create a taste for mental work and leave their imprint on mind
and character for a lifetime." George Polya, 1944
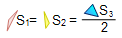HINTS:
1. CEVIAN:
A Cevian is a line segment which
joins a vertex of a triangle with a point on the opposite side
(or its extension).
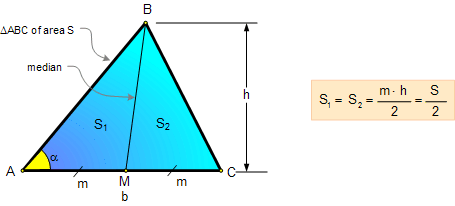
2. AREA OF A TRIANGLE:
Median Area Fact:
A median divides the triangle into
two triangles of equal area.
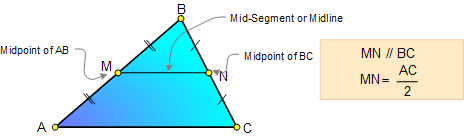
3. Mid-Segment or Midline of a
Triangle Theorem: If a line MN joins the midpoints of two
sides of a triangle, then it is parallel to the third side and
its length is one-half the length of the third side.
|
