|
In the figure below, given a triangle
ABC, Si is the area of the contact or intouch
triangle DEF, Se is the area of the extouch triangle
GHM. Prove that:
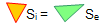 . .
HINTS:
1. The contact triangle of a triangle ABC, also
called the intouch triangle or Gergonne triangle,
is the triangle DEF formed by the points of tangency of the
incircle of triangle ABC with triangle ABC.
2.
The extouch triangle of a triangle ABC is the
triangle GHM formed by the points of tangency of the
triangle ABC with its excircles.
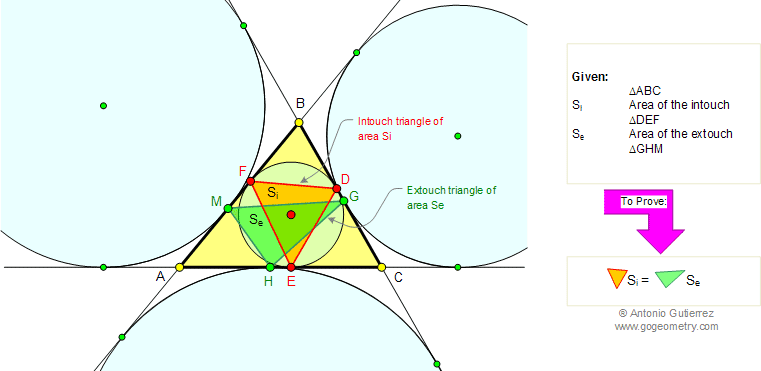
3. TANGENT TO A CIRCLE
Proposition.
Two tangent segments to a circle from an external point are
congruent.
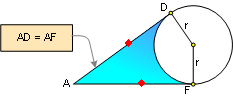
4. Semiperimeter s, Side and
Incircle Formula
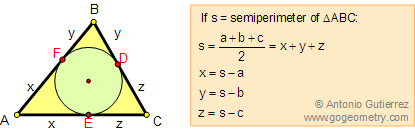
5. Semiperimeter s, Side and
Excircle Formula

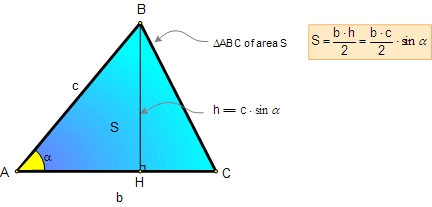
6. AREA OF A TRIANGLE:
Proposition:
The area of a triangle equals
one-half the product of the length of a side and the length of
the altitude to that side.
Side Angle Side Formula: The
SAS formula = � (side1 � side2) � sine(included angle).
6. See Problems
82,
85.
|