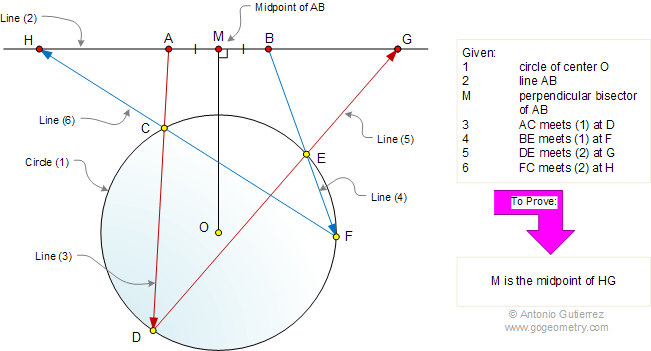
|
|
|
Given a circle (1), the lines HAMBG (2),
ACD (3), BEF (4), DEG (5),
and FCH (6). If OM is perpendicular to AB and M is the midpoint
of AB, prove that M is the midpoint of HG.
Post your solutions or ideas in the
blog.
|
HINTS:
PARALLEL LINES
Proposition. If two lines are parallel,
each pair of alternate interior angles are congruent. Also
converse.
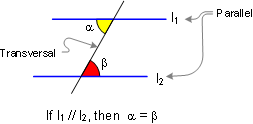
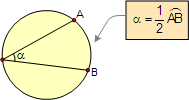
ANGLES IN A CIRCLE
Proposition. An inscribed angle is measured by
one-half its intercepted arc.
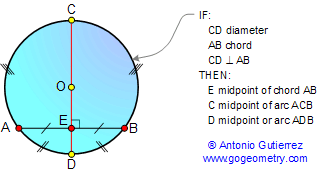
DIAMETER AND CHORD
Proposition. A diameter perpendicular to a
chord bisects the chord and its arcs..
TRIANGLE CONGRUENCE A.S.A. If two
angles and the included side of one triangle are congruent to
the corresponding parts of another, then the triangles are
congruent.
CYCLIC QUADRILATERAL is a
quadrilateral whose vertices all lie on a single circle.
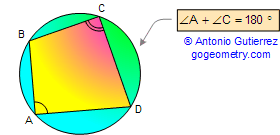
Proposition 1.
Opposite angles of a cyclic
(inscribed) quadrilateral are supplementary. Also converse.
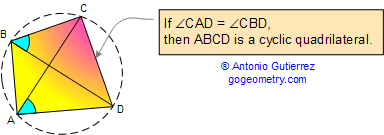
Proposition 2. A quadrilateral is cyclic if one side subtends
congruent angles at the two opposite vertices. Also
converse.
See:
Proposed
Problem 77
|
