Heron's Formula: Key Facts.Geometry Help.

Before beginning the proof of Heron's Formula, we need to be aware of the following preliminary propositions: 

DEFINITION 1. Angle Bisector is a ray that divides the angle into two congruent adjacent angles.

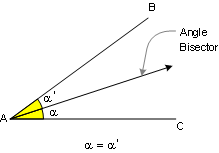
PROPOSITION 2. Triangle Congruence A.S.A. If two angles and the included side of one triangle are congruent to the corresponding parts of another, then the triangles are congruent.

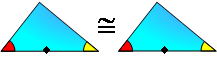
PROPOSITION 3. Any point on the bisector of an angle is equidistant from the sides of the angle.

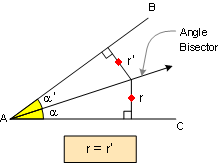
Proof: Apply Definition #1 and Proposition #2.

PROPOSITION 4. If a line is tangent to a circle, it is perpendicular to a radius at the point of tangency.

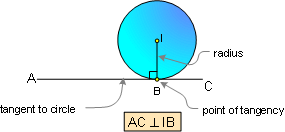PROPOSITION 5. The bisectors AA', BB' and CC' of the angles of a triangle ABC meet in a point I, which is equidistant from the sides of the triangle.

The incircle is the inscribed circle of a triangle. The center of the incircle is called the incenter, and the radius of the circle is called the inradius.

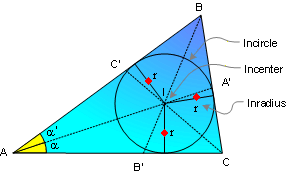
Proof: Apply Proposition #3 and #4.
 

PROPOSITION 6. An excircle of the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two.

The center of an excircle is the intersection of the internal bisector of one angle and the external bisectors of the other two.

The center of an excircle is called the excenter, and the radius of the circle is called the exradius.

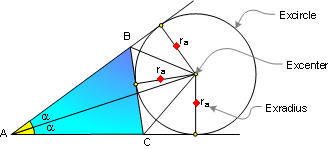
Proof: Apply Proposition #3 and #4.
 

PROPOSITION 7. Two tangent segments to a circle from an external point are congruent.

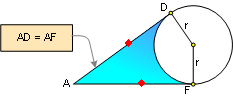
Proof: Apply Proposition #2, #3.
 

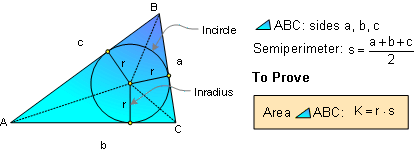
PROPOSITION 8. Semiperimeter and Incircle.

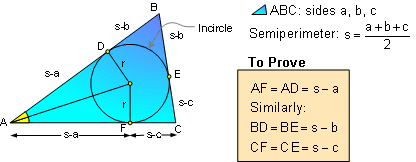
Proof: Apply Proposition # 7.
 

PROPOSITION 9. Semiperimeter and Excircle.

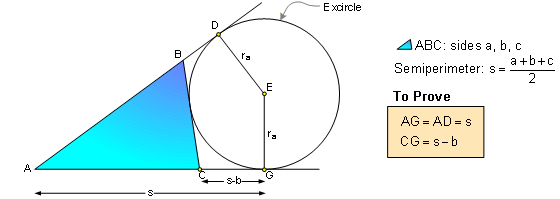
Proof: Apply Proposition # 7.
 

PROPOSITION 10. Area of any triangle.

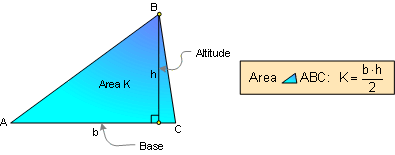
PROPOSITION 11. Area of any triangle.

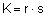
Proof: Apply Proposition #10 and #4.
 

PROPOSITION 12. Area of any triangle.

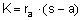
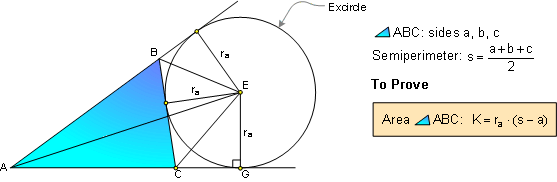
Proof: Apply Proposition #10 and #4.
 

PROPOSITION 13. Bisectors (CD and CE) of supplementary angles (FCB and BCG) are mutually perpendicular lines.

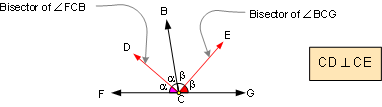
PROPOSITION 14. Two acute angles are congruent if their sides are respectively perpendicular to each other.

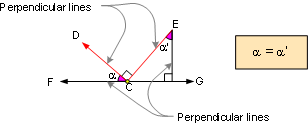PROPOSITION 15. Triangle Similarity AA. If two angles of one triangle are congruent to two angles of another triangle, the two triangles are similar.

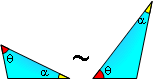
Home | Geometry | Search | Problems | Heron's Formula | Previous, Next | Email By Antonio Gutierrez
Last updated: April 19, 2008