|
41. Proposed
Problems about congruence of line segments, angles, and triangles.
Level: High School, SAT Prep, College geometry.

42.
Ptolemy's Theorem.

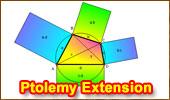
43.
Ptolemy's
Extension Cyclic Quadrilateral: Ratio of the Diagonals.
|
44. Sangaku
Problem
(An Old Japanese Theorem)
|
|
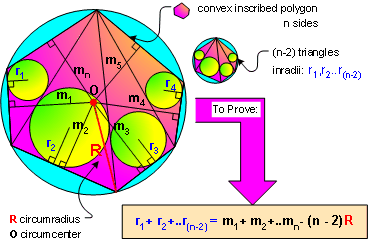
Let a convex inscribed polygon be
triangulated in any manner, and draw the
incircle
to each triangle so constructed. Then the sum of the
inradii
is a constant independent of the triangulation chosen.
|
|
|
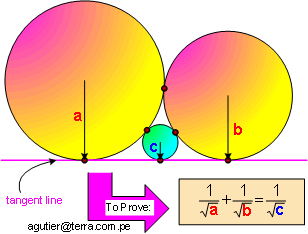
45. Sangaku Problem 2.
Proof
|
|
3 circles of radiii:
a,
b,
c
mutually
tangent to each other and a line
|
|
47.
Sawayama -Thebault's
theorem

48.
Semiperimeter and excircles of a triangle
49.
Semiperimeter and incircle of a triangle
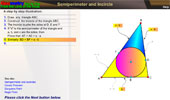
50.
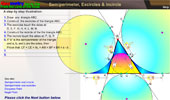
Semiperimeter and incircle and excircles of a triangle
|