Problem 687: Triangle, Three Excircles, Tangency points, Tangent lines, Concurrent Lines. Level: High School, SAT, College Geometry

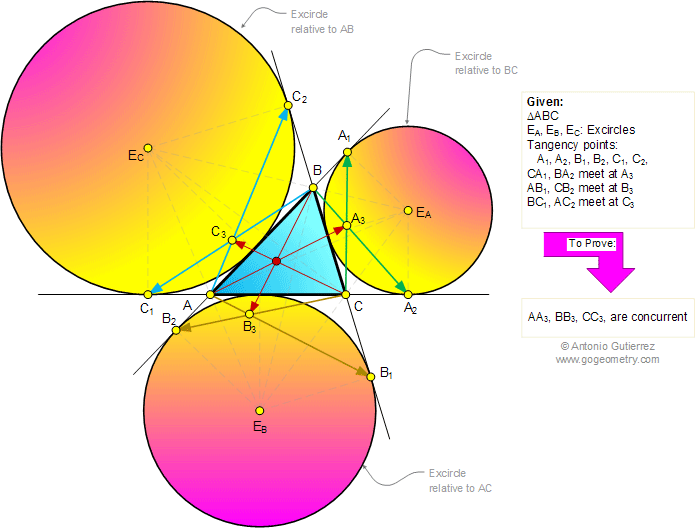
The figure shows a triangle ABC with the excircles E_A, E_B, and E_C tangent to the extension of sides at the points A₁, A₂, B₁, B₂, C₁, and C₂. Lines CA₁ and BA₂ meet at A₃, AB₁ and CB₂ meet at B₃, BC₁ and AC₂ meet at C₃. Prove that lines AA₃, BB₃, and CC₃ are concurrent.