|
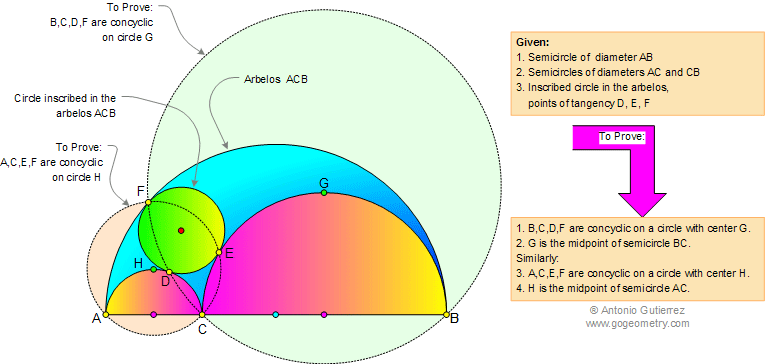
Geometry Problem 638. If a circle is inscribed in the
arbelos ACB with tangency points D, E, and F, as shown in the
figure, then the points B, C, D, and F are concyclic on circle with
center G and G is the midpoint of the semicircle of diameter BC.
Similarly, A, C, E, and F are concyclic on circle with center H and H is
the midpoint of semicircle of diameter AC.
|
|
 |
Geometry Problem 637
Semicircle, Diameter, Perpendicular, Inscribed Circle, Chord, Tangent, Arbelos. |