College Geometry Online, eLearning

Median of a Trapezoid, Theorems and Problems- Table of Content

 

Trapezoid median, Theorems and Problems, Index

  
 

Trapezoid Index

Trapezoids. Index.
 

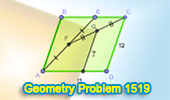Geometry Problem 1519

Geometry Problem 1519 and a Thematic Poem.
Discover the Length of a Segment in a Parallelogram using Midpoints and Parallel Lines.
 

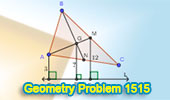Geometry Problem 1515

Geometry Problem 1515 and a Thematic Poem.
Mastering Triangle Distance Calculation: Find the Distance from the Intersection of Medians to an Exterior Line. Difficulty Level: High School.
 

Quadrilateral, midpoints

Problem 237. Quadrilateral, Midpoints, Exterior line, Perpendicular lines.
Median of a Trapezoid.
 

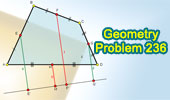Quadrilateral, midpoints

Geometry Problem 236. Quadrilateral, Midpoints, Exterior line, Perpendicular lines.
Median of a Trapezoid.

 

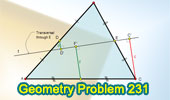Elearn 231: Triangle, Midpoint

Proposed Problem 231. Triangle, Midpoints, Transversal, Perpendicular lines.
Median of a Trapezoid.

 

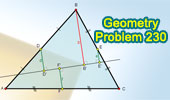Elearn 230: Triangle, Midpoint, Transversal

Geometry Problem 230. Triangle, Midpoints, Transversal, Perpendicular lines.  
 

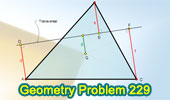Elearn 229: Triangle, Centroid, Transversal

Proposed Problem 229. Triangle, Centroid, Transversal, Perpendicular lines.
Median of a Trapezoid.  
 

Elearn 228: Triangle, Midpoint

Geometry Problem 228. Triangle, Midpoints, Exterior line, Perpendiculars lines.
Median of a Trapezoid.  
 

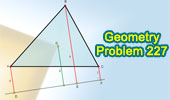Elearn 227: Triangle, Centroid

Proposed Problem 227. Triangle, Centroid, Exterior line, Perpendicular lines.
Median of a Trapezoid.  
 

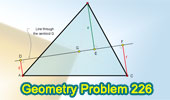Problem 226: Triangle, Centroid

Geometry Problem 226. Triangle, Centroid, Perpendiculars.
Median of a Trapezoid.  
 

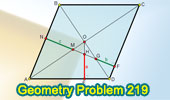Rhombus problem

Proposed Problem 219. Rhombus, perpendiculars, arithmetic mean.
Midpoints. Median of a Trapezoid.
 

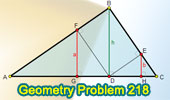Elearn 218: Right triangle

Geometry Problem 218. Right triangle, Altitude and Projections.
Midpoints. Median of a Trapezoid.
 

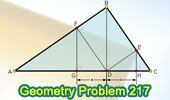Elearn 217: Right triangle, Altitude, Projections

Proposed Problem 217. Right triangle, Altitude and Projections.
Midpoints. Median of a Trapezoid.
 

Trapezoid

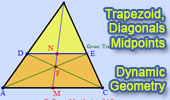Trapezoid, Triangle, Diagonals, Midpoints. Dynamic Geometry.
Step-by-Step construction, Manipulation, and animation.
Prove proposition.
 

Trapezoid, Triangle, Area

Geometry Problem 170. Trapezoid, Midpoint, Triangle, Area. Median of a Trapezoid. 
 

Geometry Problem 158

Proposed Problem 158. Relation between the Circumradius, Inradius and Exradii of a triangle. Median of a Trapezoid.

Trapezoid

TRAPEZOID: A trapezoid is a quadrilateral having two parallel sides called bases.

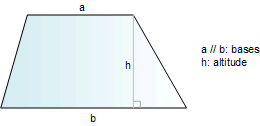
Trapezoid definition
 

SCALENE, ISOSCELES, AND RIGHT TRAPEZOID:  

 
Scalene, Isosceles, Right trapezoid


 

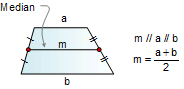
MEDIAN OF A TRAPEZOID (Midline or Midsegment):  Segment joining the midpoints of the two legs. The median is parallel to the bases and equal to one half of the sum of the bases.

 
Median of a trapezoid


 

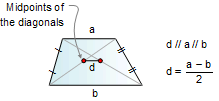
MIDPOINTS OF THE DIAGONALS:  The segment joining the midpoints of the two diagonals is parallel to the bases and equal to one half of the difference of the bases.

 
Midpoints of diagonals of a trapezoid

Post a comment
  
Home | Search | Geometry | Quadrilateral | Trapezoid | Email | By Antonio Gutierrez