|
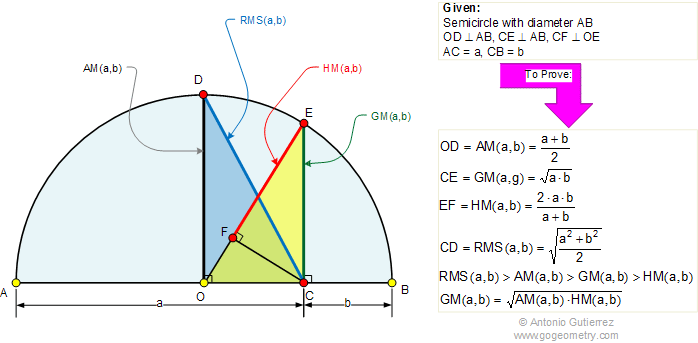
The figure above shows a semicircle with diameter AB
and center O. C is a point on AB, CE and OD are
perpendicular to AB, and CF is perpendicular
to OE. If AC = a and CB = b, prove that:
-
OD is the arithmetic mean of
a and b; AM(a,b).
-
CE is the geometric mean of
a and b; GM(a,b).
-
EF is the harmonic mean of a
and b; HM(a,b).
-
CD is the root mean square
of a and b; RMS(a,b)
-
Inequality: RMS (a,b) > AM (a,b) > GM (a,b)
> HM (a,b)
-
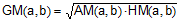 . .
|