|
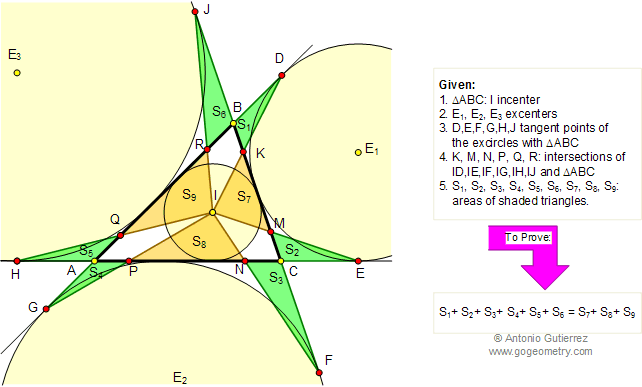
En el triangulo ABC de la figura, I es el incentro y los puntos D, E, F,
G, H, J
son los puntos de tangencia de las cirunferencias exinscritas
con las prolongaciones de los lados del triangulo ABC. ID, IE, IF, IG,
IH, y IJ intersecan a los lados del triangulo ABC en K, M, N, P,
Q, y R, respectivamente. Si S1, S2, S3,
S4, S5, S6, S7, S8,
y S9, son las Áreas de los triángulos sombreados,
demostrar que
S1+S2+S3+S4+S5+S6
= S7+S8+S9.
|