|
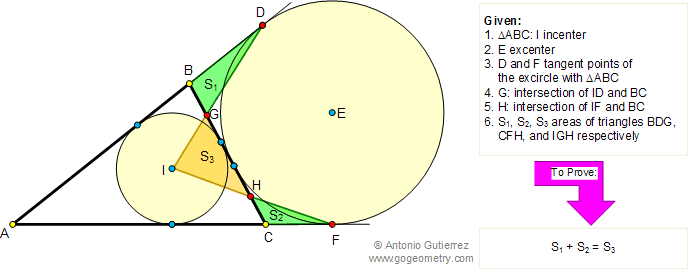
En el triangulo ABC de la figura, I es el incentro y los puntos D y F
son los puntos de tangencia de las prolongaciones de AB y AC con
la circunferencia exinscrita relativa a BC. ID y BC se intersecan en G.
IF y BC se
intersecan en H. Si S1, S2, y S3 son las áreas de los triángulos
BDG, CFH y IGH, respectivamente, demostrar que S1 + S2 = S3.
|