Geometría Dinámica, Software de Geometría Interactiva y Aplicaciones 2

Problemas de Geometría
Problemas del 1301 al 1400
Problemas del 1201 al 1300
Problemas del 1101 al 1200
Problemas del 1001 al 1100

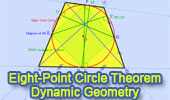Eight-Point Circle Theorem
Step-by-Step construction, Manipulation, and animation.
Dynamic Geometry.

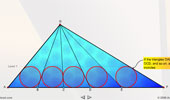
Equal Incircles Theorem. Interactive.

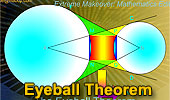Eyeball Theorem: Animated Angle to Geometry Study.

Segundo Punto Ajima-Malfatti
Ilustración Animada, Paso a Paso.

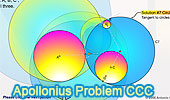Apollonius' Problem for Three Circles Interactive illustration.

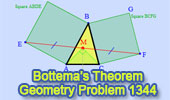Bottema's Theorem.
Invariance of an isosceles right triangle.
Triangle and Squares with Interactive Geometry Software
Step-by-Step construction, Manipulation, and animation.

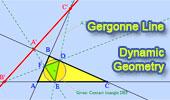Interactive Gergonne Line and Nobbs Points. Dynamic Geometry.
Step-by-Step construction, Manipulation, and animation.

Interactive Hinged tessellation. Square tessellation - Dynamic Geometry.
C.a.R. (Compass and Ruler). This Java applet requires Java 1.3 or higher.

Screencast Tutorial: Interactive Square Hinged Tessellation.
C.a.R. (Compass and Ruler).

Incenter, Excenter, Incircle, Excircle Using TracenPoche Dynamic Software
Step-by-Step construction, Manipulation, and animation.

Isogonic-Jacobi Theorem: Using TracenPoche Dynamic Geometry Software

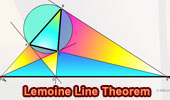Lemoine Theorem
Interactive illustration.

Marion Walter's Theorem: Triangle and Hexagon areas: Using TracenPoche Dynamic Geometry Software

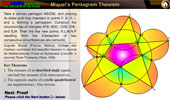Miquel's Pentagram Theorem Interactive proof with animation and key theorems.
 

Miquel's Pentagram with Dynamic Geometry. You can alter the pentagram dynamically in order to test and prove (or disproved) conjectures and gain mathematical insight that is less readily available with static drawings by hand. Requires Java Plug-in 1.3 or higher. Please be patient while the applet loads on your computer.

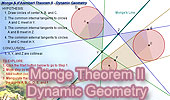Monge & d'Alembert Three Circles Theorem II with Dynamic Geometry. You can alter the geometric construction dynamically in order to test and prove (or disproved) conjectures and gain mathematical insight that is less readily available with static drawings by hand. Requires Java Plug-in 1.3 or higher. Please be patient while the applet loads on your computer.

Ir a pagina: Anterior | Siguiente