Geometry Problem 985: Circle, Radius, Perpendicular, Concentric Circles, Congruence, Triangle. Mobile Apps. Level: College, High School.

< PREVIOUS PROBLEM | NEXT PROBLEM >

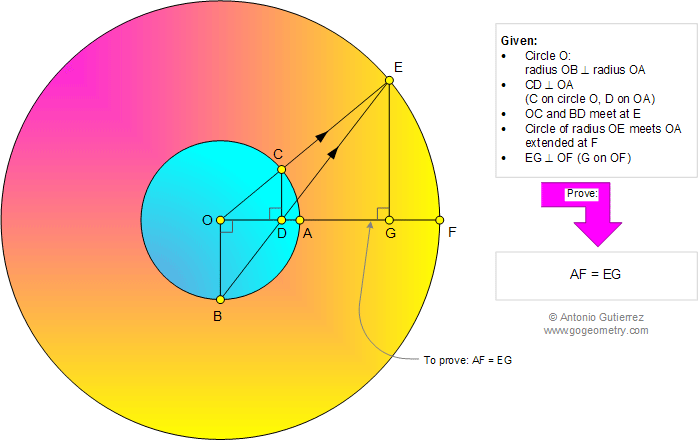
The figure below shows a circle O with radius OB perpendicular to radius OA. CD is perpendicular to OA (C on circle O, D on OA). OC and BD extended meet at E. Circle of radius OE meets OA extended at F. EG is perpendicular to OF (G on OF). Prove that AF = EG.

Geometry Problem 985: Circle, Radius, Perpendicular, Concentric Circles, CongruenceQuadrilateral, Diagonal, Triangle, Congruence, Angle Bisector

Art of Geometry Problem 985 using Mobile Apps. Circle Patterns.

Geometric art is a form of art based on the use and application of geometric figures. A geometric figure is any set or combination of points, lines, surfaces and solids. A mobile app or mobile application software is a computer program designed to run on smartphones and tablet computers.

Art of problem 985 concentric circles patterns using mobile apps, iPad, iPhone