Geometry Problem 981. Triangle, Concurrent Cevians, Midpoints, Area, Hexagon

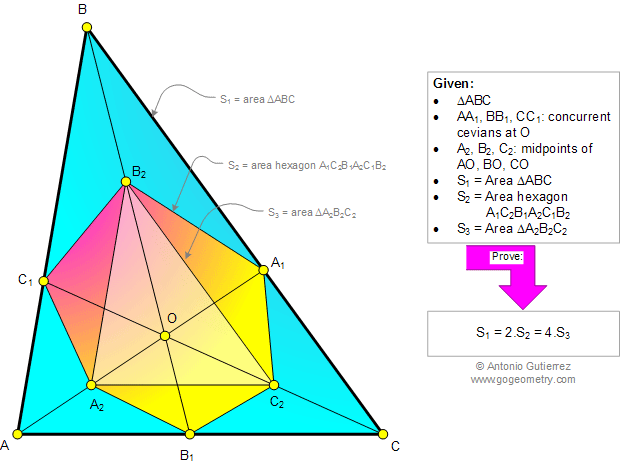
AA₁, BB₁, and CC₁ are concurrent cevians of triangle ABC at O (see the infographic below). A₂, B₂, and C₂ are the midpoints of AO, BO, and CO, respectively. If S₁ S₂ and S₃ are the areas of triangle ABC, hexagon A₁C₂B₁A₂C₁B₂, and triangle A₂B₂C₂, prove that S₁ = 2.S₂ = 4.S₃
 

Sketch of problem 981

See also:
Geometry
Problems
All Problems
Open Problems
Visual Index
10 Problems
Problems Art Gallery
Art
981-990
Triangles
Triangle Area
Hexagon
Midpoints
Concurrency
Add or view a solution to the problem 981