|
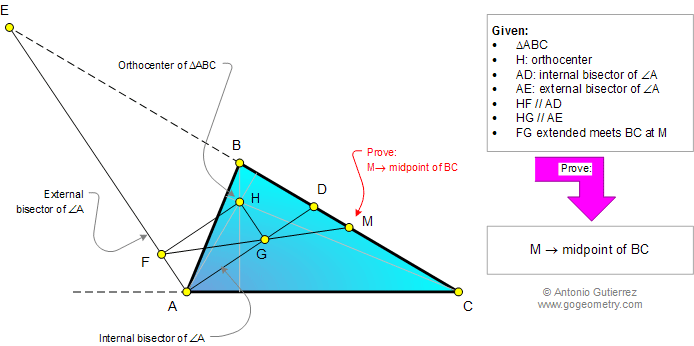
The figure shows a triangle ABC,
H is the orthocenter, AD and AE are the internal and external
bisectors of angle A. HF is parallel to AD and HG parallel to AE
(G on AD and F on AE). FG extended meets BC at M. Prove that M
is the midpoint of BC.
See also:
problem 914 in motion.
|