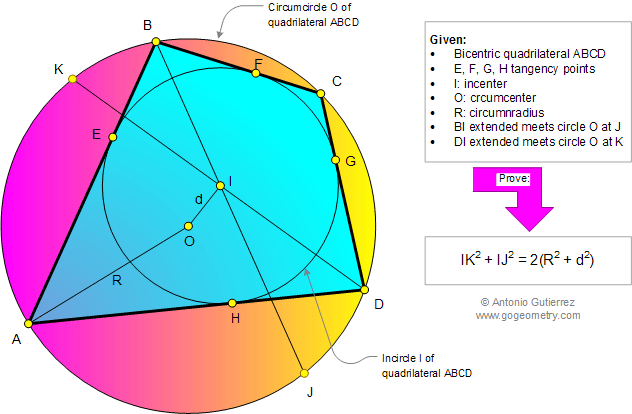
Online Geometry Problem 910: Bicentric Quadrilateral, Distance between the Incenter and Circumcenter, Incircle, Circumcircle, Circumscribed, Inscribed, Circumradius. Level: High School, College, Mathematics Education

< PREVIOUS PROBLEM | NEXT PROBLEM >

In a bicentric quadrilateral ABCD, I is the incenter, O the circumcenter, R the circumradius, and IO = d. BI and DI extended meet the circumcircle O at J and K, respectively. Prove that IK² + IJ² = 2(R² + d²).

A bicentric quadrilateral ABCD is a convex quadrilateral that has both an incircle I and a circumcircle O.

Geometry Problem 910: Bicentric Quadrilateral, Distance between the Incenter and Circumcenter, Incircle, Circumcircle, Circumscribed, Inscribed, Circumradius