Geometry Problem 1417: Triangle, Cevian, Circumcircle, Incenter, Perpendicular, Angle Bisector, Tangent Circles
Proposition
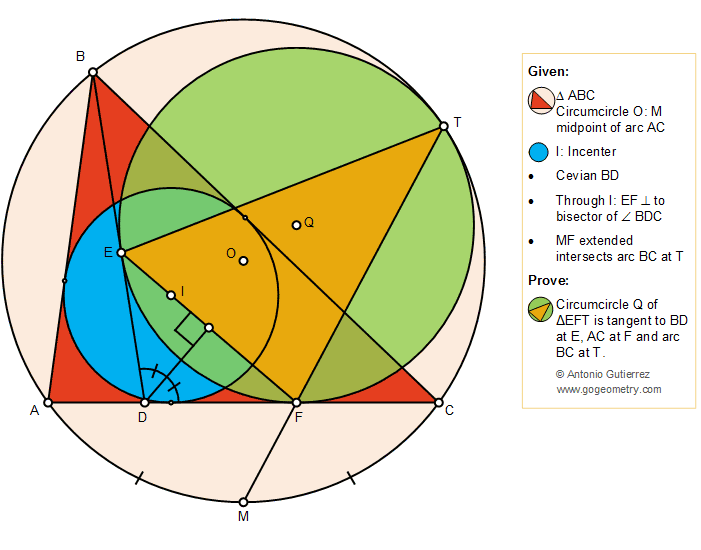
The figure below shows a triangle ABC
with the incenter I, a cevian BD, the circumcircle O and M midpoint of arc
AC. A line segment through I and perpendicular to the bisector of the
angle BDC intersects BD at E, and AC at F. MF extended intersects arc BC
at T. Prove that the circumcircle Q of the triangle EFT is tangent to BD
at E, AC at F, and arc BC at T.
Geometric Art of Problem 1417: Sketching, Typography, iPad Apps
See also: Typography and poster of problem 1408.
Search gogeometry.com
Recent Additions
Geometry Problems
Ten problems: 1411-1420
Visual Index
Open Problems
All Problems
Triangle
Circle
Incenter
Circumcircle
Tangent Line
Tangent Circles
Angle Bisector
Perpendicular lines
Midpoint
View or Post a solution