Proposition

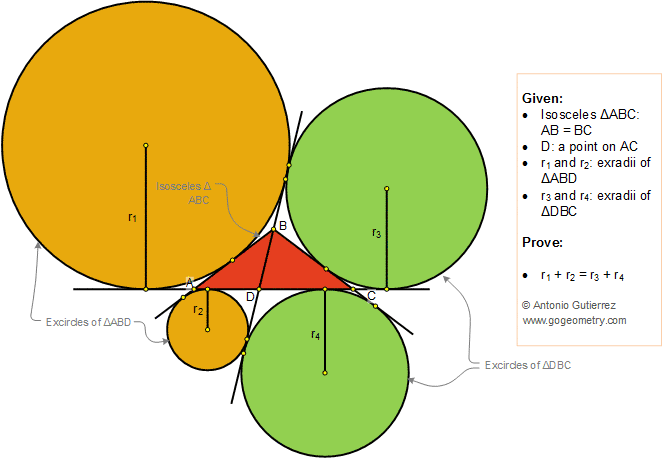
In the figure below, ABC is an isosceles triangle (AB = BC) D is a point on AC, r₁ and r₂ are the exradii of the triangle ABD corresponding to AB and AD, respectively; r₃ and r₄ are the exradii of the triangle DBC corresponding to BC and CD, respectively. Prove that r₁ + r₂ = r₃ + r₄.

BD is called an interior cevian of triangle ABC.
 

See solution below

See also:
Art of problem 1377.