Geometry Problem 1373: Isosceles Triangle, Exterior Cevian, Inradius, Exradius, Altitude to the Base.
Proposition
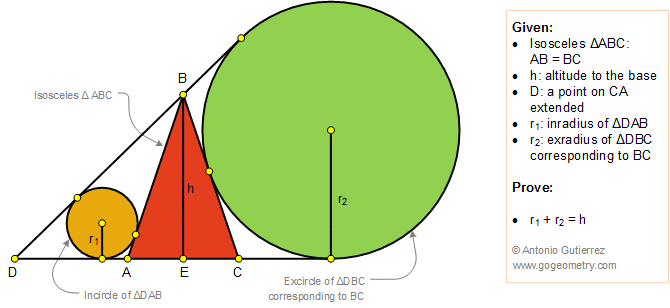
In the figure below, ABC is an isosceles triangle (AB = BC) with altitude BE = h. D is a point on CA extended, r1 is the inradius of the triangle DAB and r2 is the exradius of the triangle DBC corresponding to BC. Prove that r1 + r2 = h.
BD is called an exterior
cevian of triangle ABC.
See also:
Typography of problem 1373.
Search gogeometry.com
Recent Additions
Geometry Problems
Ten problems: 1371-1380
Visual Index
Open Problems
All Problems
Triangle
Isosceles triangle
Inradius
Exradius
Cevian
Circle
Altitude
View or Post a solution