|
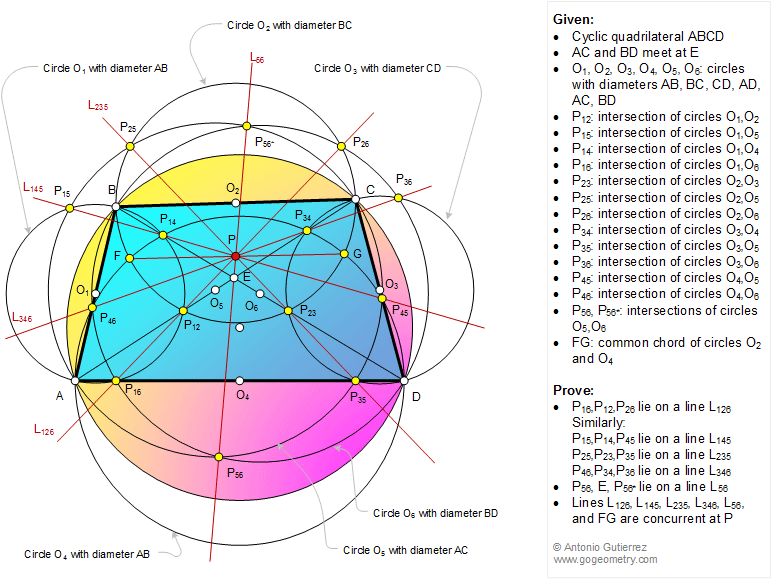
The figure shows a cyclic quadrilateral ABCD, AC and BD meet at
E. O1, O2, O3, O4, O5, O6 are circles with diameters AB, BC, CD,
AD, AC, and BD, respectively. P12, P14, P15, P16, P23, P25, P26,
P34, P35, P36, P45, P46, P56, P56* are the points of
intersection of circles O1 and O2, O1 and O4, O1 and O5, O1 and
O6, O2 and O3, O2 and O5, O2 and O6, O3 and O4, O3 and O5, O3
and O6, O4 and O5, O4 and O6, and O5 and O6, respectively.
FG is the common chord of circles O2 and O4. Prove
that (1) P16, P12, and P26 are collinear (lie on a line L126),
similarly P15, P14, and P45 are collinear (lie on a line L145),
P25, P23, and P35 are collinear (lie on a line L235), P46, P34,
and P36 are collinear (lie on a line L346); (2) P56, E,
and P56* are
collinear (line on a line L56); (3) Lines L126, L145, L235,
L346, L56, and FG are concurrent at P.
|