Geometry Problem 1107: Triangle, Circumcircle, Circle, Radius, Tangent, Chord, Congruence. Level: High School, SAT Prep, College Geometry

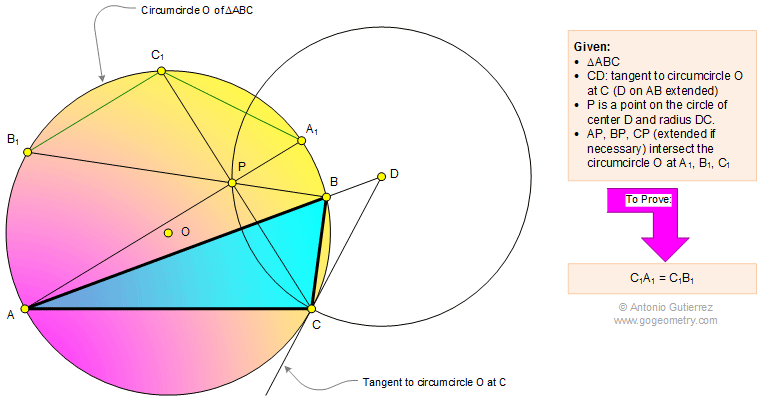
In a triangle ABC (see the figure below) CD is tangent to circumcircle O at C (D on AB extended) and P is a point on the circle of center D and radius DC. AP, BP, and CP (extended if necessary) intersect the circumcircle O at A₁, B₁, and C₁, respectively. Prove that C₁A₁ = C₁B₁.