Problem 1105: Triangle, Incircle, Excircle, Circle, Cevian, Tangent, Congruence, Geometric Mean. Level: High School, SAT Prep, College Geometry

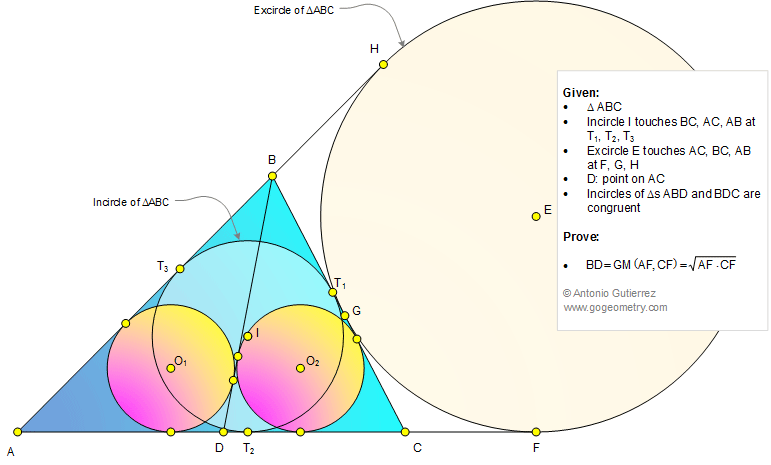
In a triangle ABC (see the figure below) the incircle I is tangent to BC, AC, and AB at T₁, T₂, and T₃. The excircle E corresponding to BC is tangent to AC, BC, and AB at F, G, and H, respectively. D is a point on AC so that the incircles of triangles ABD and BDC are congruent. Prove that BD is the geometric mean of AF and CF, that is, .
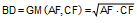