Infographic Geometry Problem 1059: Triangle, Circumcircle, Orthocenter, Altitude, Perpendicular, Reflection of a Point over a Line, Collinear Points, Simson Line, Congruence. Level: High School, SAT Prep, College, Mathematics Education

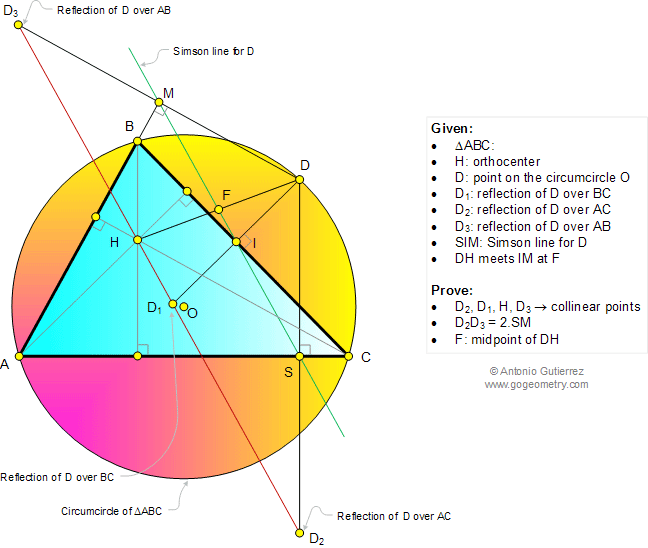
In a triangle ABC, H is the orthocenter and D is a point on the circumcircle O. D₁, D₂, and D₃ are the reflections of D over BC, AC, and AB, respectively. DH meets the Simson line for D at F. Prove that (1) D₂, D₁, H, and D₃ are collinear points; (2) D₂D₃ = 2.SM; (3) F is the midpoint of DH.