 |

|
|

How to Master Right Triangle Math: From Pythagoras to 3-D Coordinates
Comprehensive coverage of right triangle formulas, including the Pythagorean theorem, catheti, hypotenuse, altitude, projection, inradius, circumradius, exradius, semiperimeter, area, special right triangles, Poncelet's theorem,
general extension, and 2-D coordinates, as well as the Pythagorean theorem in 3-D.
|
|
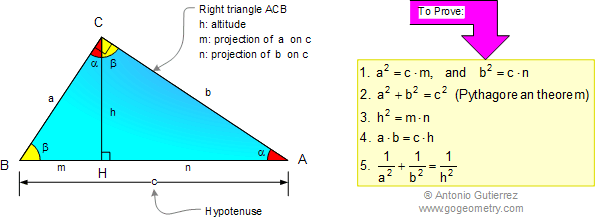
PYTHAGOREAN THEOREM, GEOMETRIC
MEAN, PRODUCT OF THE CATHETUS, ALTITUDE, PROJECTION:
Proofs that use
similarity.
|
|
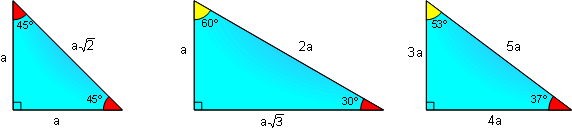
SPECIAL RIGHT TRIANGLES:
Isosceles 45-45, 30-60, 37-53 (3-4-5)
|
|
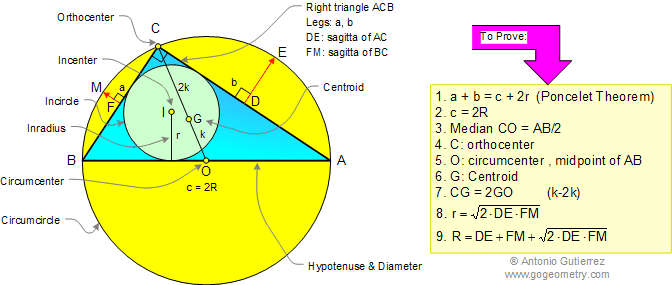
CENTERS, INRADIUS,
CIRCUMRADIUS, INCENTER, CIRCUMCENTER, ORTHOCENTER, CENTROID,
PONCELET'S THEOREM, SAGITTA.
Sagitta: The distance
between the midpoint of an arc and the midpoint of its
chord.
|
|
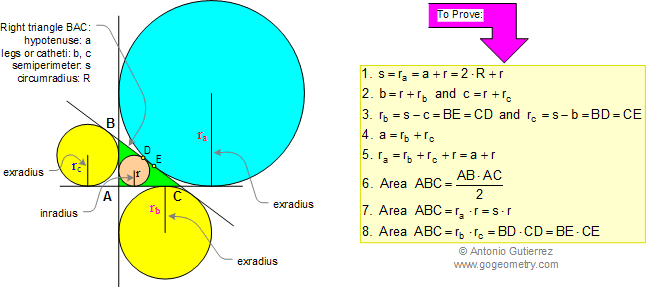
RIGHT TRIANGLE:
INRADIUS, EXRADII, SEMIPERIMETER (s), CATHETUS AND
HYPOTENUSE, AREA.
|
|
RIGHT TRIANGLE: ORTHOGONAL
PROJECTIONS
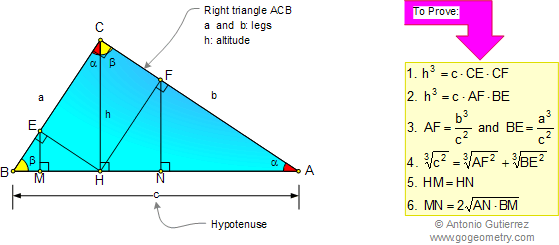
|
|
RIGHT TRIANGLE: ALTITUDE,
INRADII, INCENTER, AREAS.
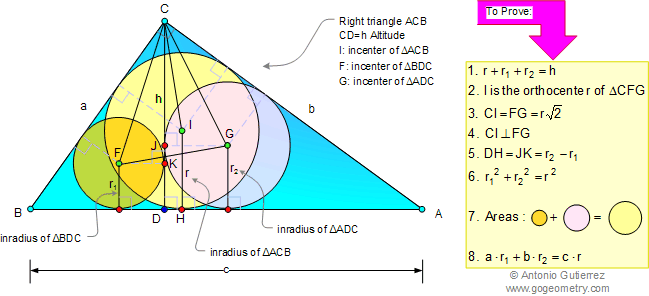
|
|
PYTHAGOREAN THEOREM: DIAGONAL OF A BOX
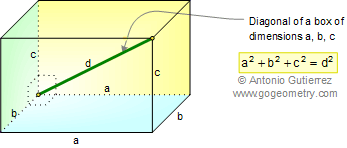
|
|
DISTANCE IN CARTESIAN
COORDINATE:
The Pythagorean Theorem provides
an easy way to compute the straight line distance between
any two points whose Cartesian coordinates are known.

|
|
PYTHAGOREAN THEOREM IN THREE DIMENSIONS 3-D, De Gua's
Theorem: In any
tetrahedron with a cubic vertex O-ABC the square
of the area of the face opposite the cubic vertex O-ABC is
equal to the sum of the squares of the areas of
the other three faces AOB, AOC, BOC.
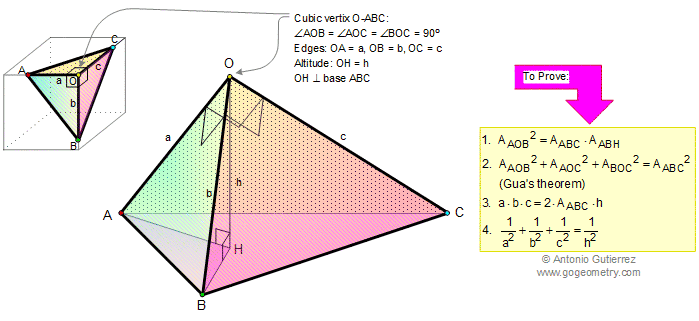
|
|
THE PYTHAGOREAN CURIOSITY: Triangles and squares, fifteen conclusions.

|
|
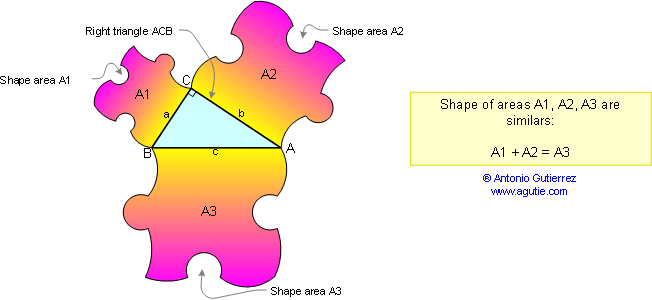
THE GENERAL EXTENSION TO
PYTHAGORAS' THEOREM: If any 3 similar shapes are drawn
on the sides of a right triangle, then the area of the shape
on the hypotenuse equals the sum of the areas on the other
two sides.
|
|
|
|
|
|
 |
 |