|
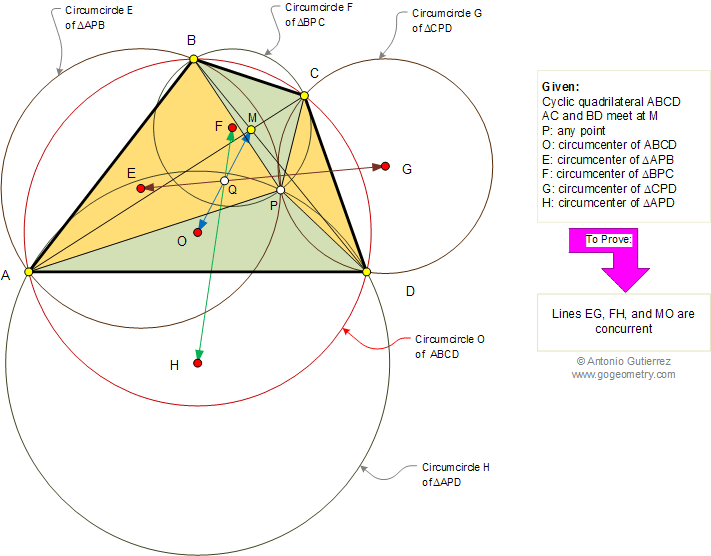
The figure shows a cyclic quadrilateral ABCD
with circumcenter O.
Diagonals AC and BD meet at M. Let P be any point inside or outside the
circle O. If E, F, G, and H are the circumcenters of
triangles APB, BPC, CPD, and APD, respectively, prove that lines EG, FH,
and MO are concurrent at the same point Q.
|