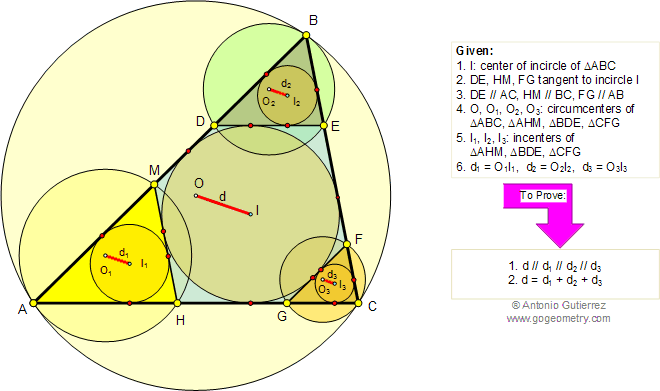
In the figure below, given a triangle ABC and the incircle of center I (inscribed circle), DE, FG, and HM are tangent to the incircle I and  parallel to AC, AB, and BC respectively. O, O₁, O₂, and O₃ are the circumcenters of triangles ABC, AHM, BDE, and CFG respectively. I₁, I₂, and I₃ are the incenters of triangles AHM, BDE, and CFG respectively. If d = OI, d₁ = O₁I₁, d₂=O₂I₂, and O₃ = O₃I₃, (1) prove that d, d₁, d₂, and d₃ are parallel, (2) prove that d = d₁ + d₂ + d₃. View or post a solution.