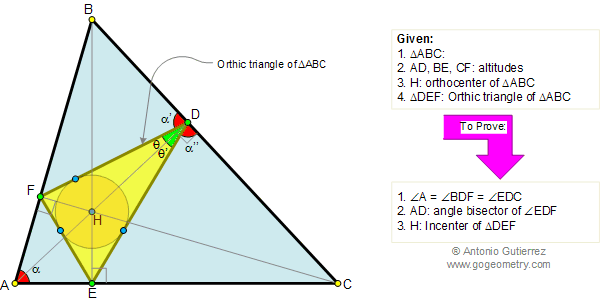
Geometry Problem 134. Orthic Triangle, Altitudes, Angle Bisectors, Orthocenter, Incenter

In the figure below, given a triangle ABC and its orthic triangle DEF (AD, BE, and CF are the altitudes of ABC). Let be H the orthocenter of ABC. (1) Prove that angles A, BDF and EDC are equal, (2) Prove that AD is the angle bisector of angle EDF, and (3) prove that H is the incenter of triangle DEF. View or post a solution.