Geometry Problem 87. Area of Quadrilateral and Midpoints of Diagonals, Median of a triangle. High School, College, Math Education

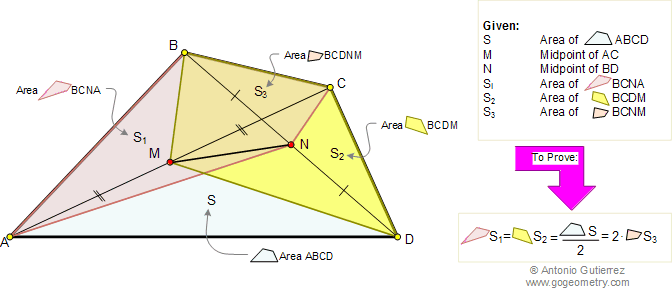
In the figure below, given a quadrilateral ABCD, M and N are the midpoints of AC and BD respectively. If S, S₁, S₂, and S₃ are the areas of the quadrilaterals ABCD,BCNA, BCDM, and BCNM respectively, prove that: \(S_1 = S_2 = \dfrac{S}{2} = 2\cdot S_3\).
 

HINTS:

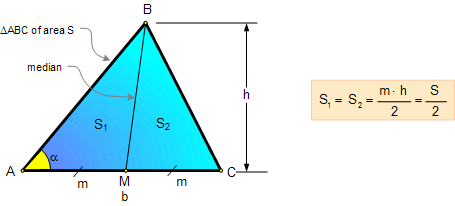
1. AREA OF A TRIANGLE:

Median Area Fact: A median divides the triangle into two triangles of equal area.

Geometric Art: Hyperbolic Kaleidoscope of problem 87 using iPad Apps.

Geometric Art using Mobile Apps

A mobile app or mobile application software is a computer program designed to run on smartphones and tablet computers.

Hyperbolic Kaleidoscope, Poincare Disk Model

Poincare disk model is a model of 2-dimensional hyperbolic geometry in which the points of the geometry are inside the unit disk, and the straight lines consist of all segments of circles contained within that disk that are orthogonal to the boundary of the disk, plus all diameters of the disk. Read more.

Tessellation

A tessellation of a flat surface is the tiling of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. Read more.

Kaleidoscope

A continually changing symmetrical pattern of shapes and colors. Read more.