|
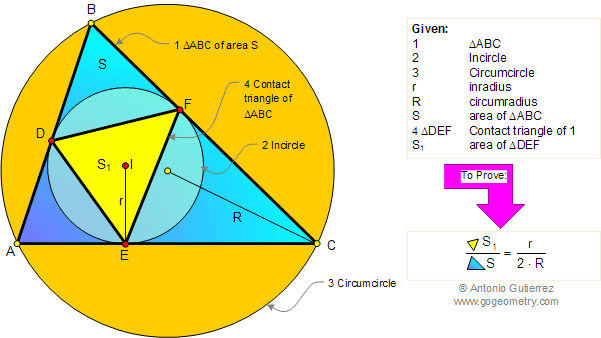
Given a triangle ABC of area S, the incircle of center I, the inradius r, and the circumradius R. If
S1 is the area of the
contact triangle DEF, prove
that: \(\dfrac{S_1}{S}=\dfrac{r}{2\cdot R}\).
See
also:
Original problem
82 art
Kaleidoscope problem
82
HINTS:
See:
Problem 81.
CONTACT TRIANGLE:
The contact triangle of a triangle
ABC (figure above), also called the intouch triangle, is the
triangle DEF formed by the points of tangency of the incircle of
triangle ABC with triangle ABC.
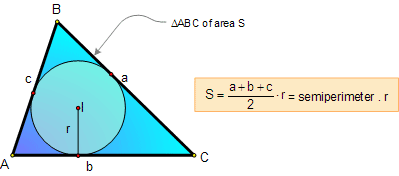
AREA OF A TRIANGLE:
Semiperimeter and Inradius
Formula
|