|
The Foundations of Geometry by David Hilbert
The book Grundlagen der Geometrie (The
Foundations of Geometry) published by Hilbert in 1899 substitutes a formal set,
comprised of 21 axioms, for the traditional axioms of Euclid. They avoid
weaknesses identified in those of Euclid, whose works at the time were still
used textbook-fashion. Hilbert's work is the cornerstone of modern geometry and
its simple, elegant, rigor has had a profound impact in many other areas of
modern science. He contributed substantially to the establishment of the
formalistic foundations of mathematics.
David Hilbert (1862-1943) was a German mathematician, recognized as one
of the most influential and universal mathematicians of the 19th and early 20th
centuries.
See also: Anschauliche Geometrie, translated into English as
Geometry and the Imagination.
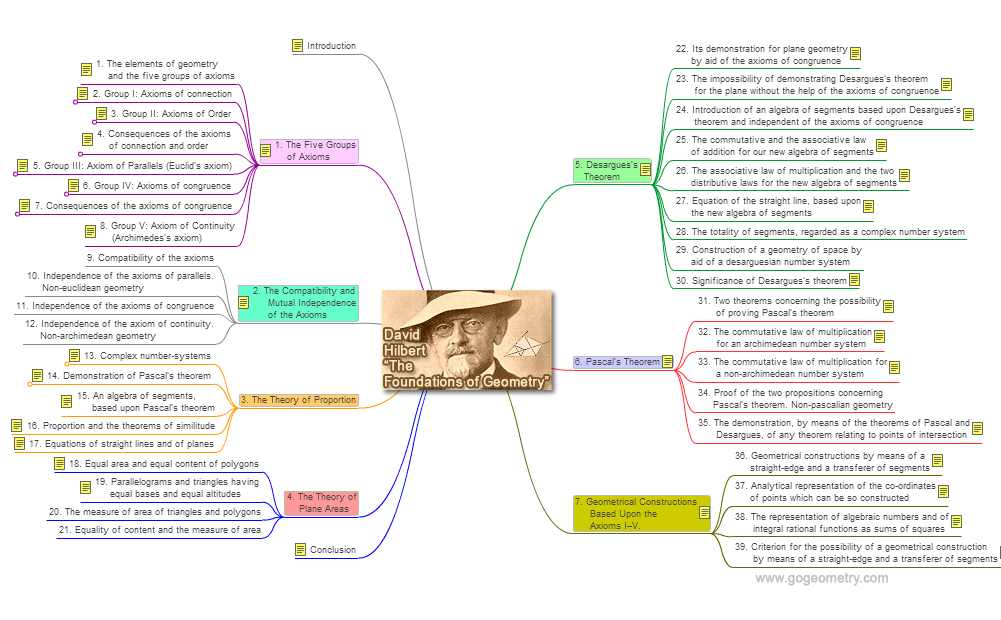
Chapters:
Introduction
1. The Five Groups of Axioms
2. The Compatibility and Mutual
Independence of the Axioms
3. The Theory of Proportion
4. The Theory of Plane Areas
5. Desargues’s Theorem
6. Pascal’s Theorem
7. Geometrical Constructions Based
Upon the Axioms I–V
Conclusion
Source: Project Gutenberg
http://www.gutenberg.org
Hilbert's famous address Mathematical Problems was
delivered to the Second International Congress of Mathematicians in Paris in
1900.
Following an extract from the address, in which
Hilbert speaks of his views on mathematics:
|
"To new concepts correspond, necessarily, new signs.
These we choose in such a way that they remind us of the phenomena which were
the occasion for the formation of the new concepts. So the geometrical figures
are signs or mnemonic symbols of space intuition and are used as such by all
mathematicians. Who does not always use along with the double inequality a > b >
c the picture of three points following one another on a straight line as the
geometrical picture of the idea "between"?
Who does not make use of drawings of segments and
rectangles enclosed in one another, when it is required to prove with perfect
rigor a difficult theorem on the continuity of functions or the existence of
points of condensation?
Who could dispense with the figure of the triangle,
the circle with its centre, or with the cross of three perpendicular axes? Or
who would give up the representation of the vector field, or the picture of a
family of curves or surfaces with its envelope which plays so important a part
in differential geometry, in the theory of differential equations, in the
foundation of the calculus of variations and in other purely mathematical
sciences?
The arithmetical symbols are written diagrams and
the geometrical figures are graphic formulas; and no mathematician could spare
these graphic formulas, any more than in calculation the insertion and removal
of parentheses or the use of other analytical signs. "
|

Mind Map: A mind map is a diagram used to
represent words, ideas, tasks or other items linked to and arranged radially
around a central key word or idea. It is used to generate, visualize, structure
and classify ideas, and as an aid in study, organization, problem solving, and
decision.
See also:
Hilbert's problems, List of twenty-three problems in 1900
Geometry and the Imagination by D. Hilbert and S. Cohn-Vossen
Last updated: Aug 2, 2014.
|
![]() .
Click and drag to move map. Click a red
arrow button to follow links. Click the
.
Click and drag to move map. Click a red
arrow button to follow links. Click the
![]() RESET
button below to center the map. Click a
branch to Fold/Unfold branches.
RESET
button below to center the map. Click a
branch to Fold/Unfold branches.