iPad Apps: Geometry Designer Illustration: Four Circles Theorem with Dynamic Geometry. Concyclic Points, Cyclic Quadrilateral, Intersection Points, Common Chord. Level: High School, College. Geometry Problem 756

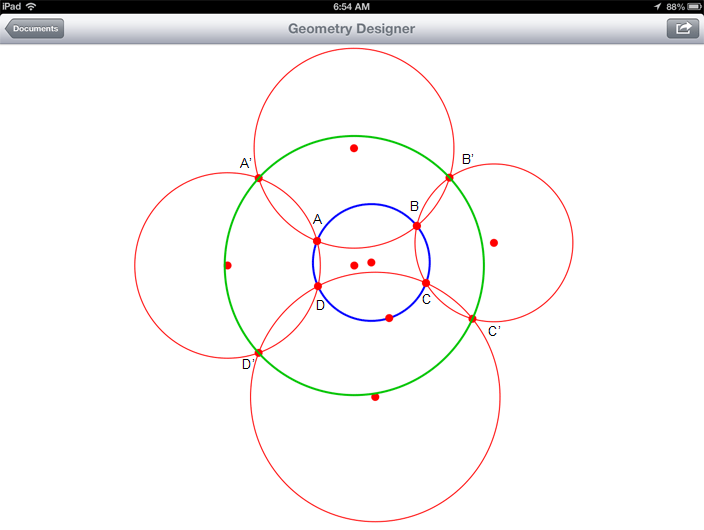
Given four concyclic points (lie on the same circumference) A,B,C,D, if four circles through AB, BC, CD, and AD are drawn, prove that the remaining four intersections points A', B', C', and D' of successive circles are concyclic.

The figure below was created using the Geometry Designer for iPad.

iPad Apps: Geometry Designer Illustration: Four Circles Theorem with Dynamic Geometry. Concyclic Points, Cyclic Quadrilateral, Intersection Points, Common Chord, Problem 756

Geometry Designer for iPad and iPhone
Geometry Designer is an apps for Math Education on iPad, iPhone and iPod, by McTavish Solutions LLC.

Geometry Designer is an exciting app that allows you to draw traditional geometric figures that you might see in a high school or college math class.

You can draw points, lines, line segments, rays, circles, arcs, and polygons. For constructions you can make angle bisectors, intersections, midpoints, and perpendicular lines. You can take measurements of angles, lengths, areas, circumferences, arc lengths, and distances.

Download on the App Store: Geometry Designer - McTavish Solutions LLC.