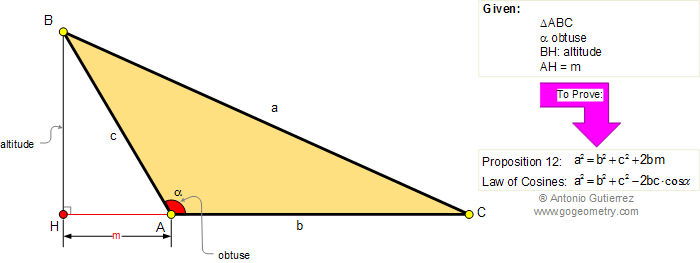
In obtuse-angled triangles (BAC) the square on the side opposite the obtuse angle (BC) is greater than the sum of the squares on the sides containing the obtuse angle (AB and AC) by twice the rectangle contained by one of the sides about the obtuse angle (AC), namely that on which the perpendicular falls, and the straight line cut off outside by the perpendicular towards the obtuse angle (AH). This conclusion is equivalent to the law of cosines.